조글로카테고리 : 블로그문서카테고리 -> 문학
나의카테고리 : 보물 + 뒷간
피보나치 수열은 자연을 닮았다고 합니다. 자연을 닮은 수가 있다니 신기하군요. 피보나치 수열이 무엇인가요? 그리고 어떻게 자연을 닮았는가요?
피보나치 수열이 뭔가요?
이탈리아의 수학자 피보나치(1170~1250)는1202년 토끼의 번식과 관련된 재미있는 문제를 소개했습니다.
“갓 태어난 토끼 한 쌍은 2개월 후부터 매달 한 쌍의 새끼 토끼를 낳습니다. 새로 태어난 토끼도 마찬가지입니다. 암수 토끼 한 쌍이 죽지 않고 계속 번식한다고 하면, 1년 뒤에는 모두 몇 쌍의 토끼가 있을까요?”
이 문제를 표로 정리하면 다음과 같습니다.
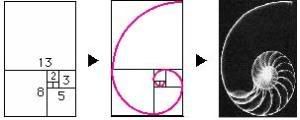
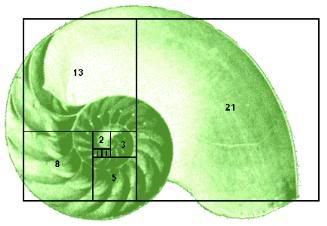
매달 전체 토끼 암수 쌍의 수를 수열로 나타내면 1, 1, 2, 3, 5, 8, 13, 21, ··· 과 같이 되는데, 이것이 바로 피보나치 수열입니다. 물론 12개월 후에는 233쌍이 됩니다.
자연에도 피보나치 수열은 존재한다
자연에는 흥미로운 수가 많습니다. 그냥 평범해 보이는 식물에도 놀라운 수학이 숨어 있을 때가 있지요. 솔방울과 해바라기가 한 예입니다. 솔방울을 뒤에서 자세히 보면, 시계 방향과 반시계 방향으로 나선이 나 있습니다. 이 나선의 개수를 세어 보면 8과 13입니다. 무엇이 신기하냐고요? 그럼 해바라기 씨를 한 번 보기로 해요. 해바라기 씨에도 솔방울처럼 시계 방향과 반시계 방향으로 나선이 있습니다. 해바라기 씨는 좀 복잡하니 꼼꼼히 세어 보아야 합니다. 나선이 시계 방향으로 34개, 반시계 방향으로 55개가 있습니다.
그렇다면 꽃잎은 어떨까요? 붓꽃은 3장, 채송화는 5장, 코스모스는 8장, 금잔화는 13장, 치커리는 21장, 질경이는 34장, ··· 의 꽃잎이 달려 있습니다.
-
- 1자란(꽃잎 3장)
- 2괭이밥(꽃잎 5장)
- 3코스모스(꽃잎 8장)
그렇다면 왜 식물의 열매나 꽃잎, 잎차례와 같은 것들은 피보나치 수열을 따르고 있는 것일까요? 그건 피보나치 수열이 자연을 닮았기 때문입니다. 식물은 다양한 형태로 씨앗을 보호하거나 번식을 하려 합니다. 그럴 때 가장 편리한 것이 바로 피보나치 수열의 수입니다. 해바라기의 씨앗도 가장 좁은 공간에 최대한 많은 양의 씨를 품으르면 피보나치 수열의 수가 되어야 한다는 것이지요.
음악도 피보나치 수열을 따른다
피아노에는 흰색과 검은색 건반이 있습니다. 검은 건반은 2개 또는 3개씩 놓여 있어요. 또 한 옥타브(도, 레, 미, 파, 솔, 라, 시, 도)에는 흰 건반이 8개, 검은 건반이 5개이고, 건반은 모두 13개입니다. 이 수들을 작은 수부터 차례로 늘어놓으면 2, 3, 5, 8, 13입니다.
2+3=5, 2+5=8, 5+8=13이므로 앞의 두 수를 더하면 그 다음 수가 되는 것을 알 수 있어요. 이러한 수의 배열을 피보나치 수열이라고 하는데, 피아노 건반에는 피보나치 수열이 숨어 있었네요.
벨라 바르톡(1881~1945)은 피보나치 수열을 음악에 충분히 활용한 작곡가입니다. 바르톡은 피보나치 수열에 따라 음악의 마디를 나누고 황금분할점2) 에 클라이맥스3) 를 두는 새로운 기법의 음악을 만들어 냈습니다. 수학과 음악을 절묘하게 조화시킨 것이지요.
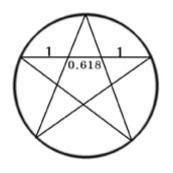
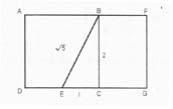
피보나치 수열은 황금비와 어떤 관계가 있나요?
피보나치 수열은 1, 1, 2, 3, 5, 8, 13, 21, ···이다. 피보나치 수열을 이용하여 분수를 계속 만들어 가면 황금비(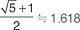
가장 아름답고 균형 있게 느껴진다는 황금비! 피보나치 수열이 황금비를 이루고, 자연은 피보나치 수열을 닮았다. 이처럼 피보나치 수열이 자연과 닮은 것은 우연히 아니라 수학이 자연의 일부이기 때문은 아닐까?
===================================================
자연의 구조 속에서 자주 발견되는 흥미로운 수열이 1202년 이탈리아의 수학자 피사의 레오나르드(Leonardo of Pisa, Fibonaci라고도 알려진)에 의해 발견되었다. 그는 태어나서 한 달 후에 새끼를 낳을 수 있는 토끼 한 쌍이 매달 새끼 한 쌍을 낳는다면 1년에 몇 마리가 되는지를 알아보는 문제에 도전했다. 레오나르도는 한 쌍이 한 달 후에 한 쌍의 토끼를 낳으면 토끼 쌍의 수는 (1, 1)이 되고 두 번째 달에는 두 쌍을 더 낳게 되어 토끼 쌍의 수는 (1, 1, 2)가 된다는 것을 알게 되었다.
이런 계산을 계속 해나가면 이전 수의 합이 다음 수가 되는 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 등으로 이루어진 수열을 얻을 수 있다. 이것이 피보나치 수열이다.
놀랍게도 피보나치 수열은 꽃잎의 배열, 솔방울의 구조(아래 그림 참조)와 같이 자연계에서 흔하게 발견된다. 그중에서도 8개의 열이 좌측으로 돌고 13개의 열이 우측으로 도는 구조로 되어 있는 파인애플은 살아 있는 피보나치의 기념비이다.
=======================================================




















[필수입력] 닉네임
[필수입력] 인증코드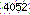 왼쪽 박스안에
표시된 수자를 정확히 입력하세요.
왼쪽 박스안에
표시된 수자를 정확히 입력하세요.